Many students are aware of HCF or LCM as distinct subjects, yet are confused when they see both in the same essay. This can lead to confusion, slow calculation, and marks that are lost. The good news is that it's simple. There is a clear mathematical connection between the two concepts.
This blog discusses the relation between HCF and LCM in plain English by using the logic of real-life examples as well as academic references that have been verified. This blog helps students tackle problems faster and with greater confidence.
What Is HCF and Why Is It Important for Students?
HCF stands for Highest Common Factor. It is the most significant number that divides two numbers in a complete way and leaves no remainder. HCF provides the strongest connections between numbers.
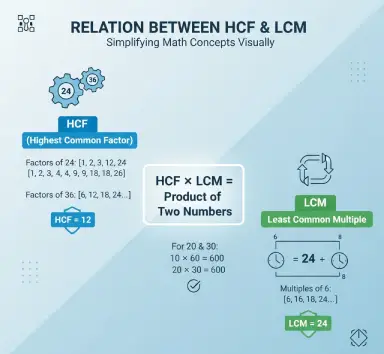
For instance, consider 24 and 36. The factors that make up 24 are 1, 2, 3, 4, 6, 12, and 24.
The 36 factors include 1, 2, 3, 4, 6, 9, 12, 18, and 36.
The most commonly used number is 12.
HCF aids in:
- Simplifying fractions
- Divide items equally
- Reducing ratios
NCERT emphasizes factor understanding as an essential math numeracy requirement in schools.
What Is LCM and How Does It Work in Daily Math?
LCM means Least Common Multiple. It is the smallest number divisible by two numbers without leaving a gap. LCM is focused on alignment and repetition.
For instance, think about the numbers 6 and 8.
Multiples of 6 are 6, 12, 18, 24...
Multiples of 8 are 8, 16, 24...
The smallest common multiple is 24, and it becomes the LCM.
LCM plays a significant role in:
- Problems with time and work
- Scheduling repeated events
- Pattern-based questions
What Is the Relation Between HCF and LCM in Simple Words?
The relation between HCF and LCM connects the largest and smallest common quantities of two values with one consistent rule:
HCF × LCM = Product of the two numbers
This rule only applies to two positive whole numbers. It helps reduce the time spent on calculations and allows students to verify their answers quickly. Teachers from all educational boards depend on this rule since it is always effective when used in a correct manner.
Understanding this relationship improves clarity and reduces confusion from the number-related issues.
HCF and LCM Mathematically
It is believed that the relation between HCF and LCM is because both of them are dependent upon the prime factorization.
Example using 20 and 30:
20 = 22 x 5
30 = 2 x 3 x 5
HCF = 2 x 5 = 10
LCM = 22 x 3 x 5 = 60
Then apply the formula:
10 x 60 = 600
20 x 30 = 600
Both results are in line, proving the relationship between HCF and LCM mathematically and numerically.
This consistency is the foundation of all the theories on numbers taught in schools around the world.
Why the Relation Between HCF and LCM Matters in Exams
The relation between HCF and LCM helps to reduce time and mistakes during tests. Instead of having to calculate the two values in isolation, students can find one and calculate the other quickly.
The key benefits are:
- Speedier problem solution
- Greater accuracy
- Stronger number sense
- Increased reasoning logically
The NCERT curriculum frameworks emphasize the importance of relationships as a key element to long-term success with math
Real-Life Applications of the Relationship Between HCF and LCM
The relationship between HCF and LCM is usually observed in real-world situations.
Common examples include:
- Equally dividing items among groups
- Planning event schedules
- Coordination of tasks that are repeated
- Controlling production cycles
For example, LCM helps predict when two schedules will align, and HCF assists in distributing resources evenly. This practical application explains that the relationship between HCF and LCM is relevant even beyond the pages of textbooks.
How to Use the Relation Between HCF and LCM Step by Step
Students can use an easy and reliable procedure:
- Find the HCF for the two numbers.
- Multiply the numbers given
- Divide the product by the HCF
- The resulting number is known as the LCM
Many e-learning platforms in India teach this method using images and guided practice
This improves the speed and increases confidence.
Common Mistakes While Using the Relationship Between HCF and LCM
Although it is simple, learners usually make costly mistakes.
Common errors include:
- The formula can be applied to more than two figures
- Utilizing fractions instead of whole numbers. Use fractions instead of whole numbers
- Confusion of HCF with the smallest of factors
NCERT explicitly states that this formula is only applicable for two positive integers.
Understanding these limitations can prevent confusion in the mind.
How Digital Learning Helps Students Master HCF and LCM
Modern educational tools are focused on the clarity of learning rather than memorization. Platforms such as the AAS Vidyalaya employ step-by-step instructions, visual breakdowns, and practice exercises to improve understanding
This type of instruction aids students in understanding the reasoning behind the relationship between HCF and LCM in lieu of using rote learning methods.
FAQs
What is the relation between the HCF and LCM of two numbers?
The relation between HCF and LCM declares that their products are the product of both numbers given, as long as both are positive integers.
How does the relationship between HCF and LCM help students?
The relationship between HCF and LCM saves time in exams and reduces calculation steps, making problem-solving faster and more accurate.
Is the relation between HCF and LCM valid for three numbers?
It is not true that the relation between HCF and LCM is only applicable to two numbers and is not directly applicable to three or more values.
Why is the relationship between HCF and LCM important in math?
The relationship between HCF and LCM builds solid number sensing and can support advanced topics such as math and problem-solving.
Conclusion
The relation between HCF and LCM links two important math concepts into one solid rule. This makes calculations easier, increases accuracy, and improves logical thinking.
From exams at school to real-world planning, the relationship between HCF and LCM proves its worth repeatedly. Once you understand it, it transforms doubt into certainty